Angle of Departure at a Pole MCQ Quiz - Objective Question with Answer for Angle of Departure at a Pole - Download Free PDF
Last updated on Feb 8, 2024
Latest Angle of Departure at a Pole MCQ Objective Questions
Angle of Departure at a Pole Question 1:
Consider the open-loop transfer function \(G\left( s \right)H\left( s \right) = \frac{K}{{s\left( {{s^2} + 6s + 25} \right)}}\). The angle of departure at the complex pole with positive imaginary part (angle measured in the anticlockwise direction and to be answered in between 0 and 360) in degrees is _______
Answer (Detailed Solution Below) 319 - 327
Angle of Departure at a Pole Question 1 Detailed Solution
\(G\left( s \right)H\left( s \right) = \frac{K}{{s\left( {{s^2} + 6s + 25} \right)}}\)
Poles: s = 0,s = -3 + 4j, -3 – 4j
At s = -3 + 4j
\(G\left( s \right)H\left( s \right) = \frac{K}{{\left( { - 3 + 4j} \right)\left( {{{\left( { - 3 + 4j} \right)}^2} + 6\left( { - 3 + 4j} \right) + 25} \right)}}\)
\( = \frac{K}{{\left( { - 3 + 4j} \right)\left( {9 - 16 - 12j - 18 + 24j + 25} \right)}}\)
\(= \frac{K}{{\left( { - 3 + 4j} \right)\left( {12j} \right)}}\)
\(= \frac{K}{{\left( { - 48 - j36} \right)}}\)
\(\angle G\left( s \right)H\left( s \right) = - \left[ {180 + {{\tan }^{ - 1}}\left( {\frac{{36}}{{48}}} \right)} \right]\)
= -216.86
Angle of departure = 180 + (-216.86)
= -36.86°
= 323.14°
Angle of Departure at a Pole Question 2:
The open-loop transfer function of a system \(G\left( s \right)H\left( s \right) = \frac{{K\left( {{s^2} + 4s + 5} \right)}}{{\left( {{s^2} + 2s + 5} \right)}}\). The angle of departure at s = -1 + 2j is:
Answer (Detailed Solution Below)
Angle of Departure at a Pole Question 2 Detailed Solution
Concept:
The angle of departure: It is the angle at which the root locus originates from the open-loop pole. It is calculated only for those poles which will locate in the complex plane.
It is calculated as, θd = 180o - (фP - фZ)
Where фP is the total angle subtended by the remaining open-loop poles towards that complex pole whose departure angle we are calculating
ФZ is the total angle subtended by all the open-loop zeroes towards the complex pole whose departure angle we are calculating.
Calculation:
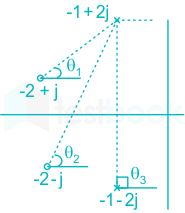
Poles: s2 + 2s + 5 = 0
⇒ s = -1 + 2j, -1 – 2j
Zeros: s2 + 4s + 5 = 0
⇒ z = s = -2 + j, -2 – j
Angle of departure θd = 180° - (ϕp - ϕz)
\({\theta _1} = {\tan ^{ - 1}}\left( {\frac{{1 - 2}}{{ - 2 + 1}}} \right) = 45^\circ \)
\({\theta _2} = {\tan ^{ - 1}}\left( {\frac{{ - 1 - 2}}{{ - 2 + 1}}} \right) = {\tan ^{ - 1}}3 = 71.59^\circ \)
θ3 = 90°
ϕp = θ3 = 90°
ϕz = θ1 + θ2 = 45 + 71.57 = 116.57°
θd = 180° - (ϕp - ϕz)
θd = 180° - [90° - 116.57°]
θd = 206.56°
Top Angle of Departure at a Pole MCQ Objective Questions
Angle of Departure at a Pole Question 3:
Consider the open-loop transfer function \(G\left( s \right)H\left( s \right) = \frac{K}{{s\left( {{s^2} + 6s + 25} \right)}}\). The angle of departure at the complex pole with positive imaginary part (angle measured in the anticlockwise direction and to be answered in between 0 and 360) in degrees is _______
Answer (Detailed Solution Below) 319 - 327
Angle of Departure at a Pole Question 3 Detailed Solution
\(G\left( s \right)H\left( s \right) = \frac{K}{{s\left( {{s^2} + 6s + 25} \right)}}\)
Poles: s = 0,s = -3 + 4j, -3 – 4j
At s = -3 + 4j
\(G\left( s \right)H\left( s \right) = \frac{K}{{\left( { - 3 + 4j} \right)\left( {{{\left( { - 3 + 4j} \right)}^2} + 6\left( { - 3 + 4j} \right) + 25} \right)}}\)
\( = \frac{K}{{\left( { - 3 + 4j} \right)\left( {9 - 16 - 12j - 18 + 24j + 25} \right)}}\)
\(= \frac{K}{{\left( { - 3 + 4j} \right)\left( {12j} \right)}}\)
\(= \frac{K}{{\left( { - 48 - j36} \right)}}\)
\(\angle G\left( s \right)H\left( s \right) = - \left[ {180 + {{\tan }^{ - 1}}\left( {\frac{{36}}{{48}}} \right)} \right]\)
= -216.86
Angle of departure = 180 + (-216.86)
= -36.86°
= 323.14°
Angle of Departure at a Pole Question 4:
The open-loop transfer function of a system \(G\left( s \right)H\left( s \right) = \frac{{K\left( {{s^2} + 4s + 5} \right)}}{{\left( {{s^2} + 2s + 5} \right)}}\). The angle of departure at s = -1 + 2j is:
Answer (Detailed Solution Below)
Angle of Departure at a Pole Question 4 Detailed Solution
Concept:
The angle of departure: It is the angle at which the root locus originates from the open-loop pole. It is calculated only for those poles which will locate in the complex plane.
It is calculated as, θd = 180o - (фP - фZ)
Where фP is the total angle subtended by the remaining open-loop poles towards that complex pole whose departure angle we are calculating
ФZ is the total angle subtended by all the open-loop zeroes towards the complex pole whose departure angle we are calculating.
Calculation:

Poles: s2 + 2s + 5 = 0
⇒ s = -1 + 2j, -1 – 2j
Zeros: s2 + 4s + 5 = 0
⇒ z = s = -2 + j, -2 – j
Angle of departure θd = 180° - (ϕp - ϕz)
\({\theta _1} = {\tan ^{ - 1}}\left( {\frac{{1 - 2}}{{ - 2 + 1}}} \right) = 45^\circ \)
\({\theta _2} = {\tan ^{ - 1}}\left( {\frac{{ - 1 - 2}}{{ - 2 + 1}}} \right) = {\tan ^{ - 1}}3 = 71.59^\circ \)
θ3 = 90°
ϕp = θ3 = 90°
ϕz = θ1 + θ2 = 45 + 71.57 = 116.57°
θd = 180° - (ϕp - ϕz)
θd = 180° - [90° - 116.57°]
θd = 206.56°
Angle of Departure at a Pole Question 5:
What is the value of the departure angle of root locus from the complex pole at s = -2 + j for
\(G\left( s \right)H\left( s \right) = \frac{K}{{\left( {s + 1} \right)\left( {s + 2 - j} \right)\left( {s + 2 + j} \right)}}\)
Answer (Detailed Solution Below) -44 - -46
Angle of Departure at a Pole Question 5 Detailed Solution
Angle of departure is given by,
θD = 180° + ∠G(s)H(s) (or) 180° - ϕ
ϕ = (∠ poles - ∠ zeros) of G(s)H(s)
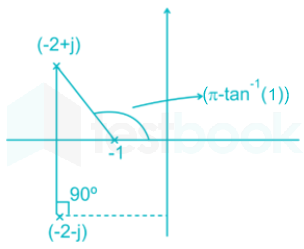
θD = 180° - 90 – (π – tan-1 (1))
= -90 + tan-1(1) = -45°Angle of Departure at a Pole Question 6:
The open loop transfer function of a system is \(G\left( s \right)H\left( s \right) = \frac{K}{{s\left( {{s^2} + 2s + 2} \right)}}\). Then the modulus of angle of departure at the complex pole is ___________ (degrees)
Answer (Detailed Solution Below) 45
Angle of Departure at a Pole Question 6 Detailed Solution
\(\begin{array}{l} G\left( s \right)H\left( s \right) = \frac{K}{{s\left( {{s^2} + 2s + 2} \right)}}\\ = \frac{K}{{s\left( {s + 1 + i} \right)\left( {s + 1 - i} \right)}} \end{array}\)
angle of departure \({\left. {{\emptyset _d} = 180^\circ + \angle GH} \right|_{s = \left( { - 1 + j} \right)}}\)
\(\begin{array}{l} {\left. {\angle GH} \right|_{s = \left( { - 1 + j} \right)}} = \frac{K}{{\angle \left( { - 1 + j} \right).\angle 2j.\angle 0}}\\ = - \left( {\pi - \frac{\pi }{4}} \right) - \frac{\pi }{2} = - 225^\circ \\\phi _d = 180^\circ - 225^\circ = - 45^\circ \end{array}\)
Modulus of Φd = 45
Angle of Departure at a Pole Question 7:
The feedback configuration and the pole-zero locations of
\(G\left( s \right) = \frac{{{s^2} - 2s + 2}}{{{s^2} + 2s + 2}}\)
are shown below. The root locus for negative values of k, i.e. for -∞ < k < 0, has breakaway / break-in points and angle of departure at pole P (with respect to the positive real axis) equal to
Answer (Detailed Solution Below)
Angle of Departure at a Pole Question 7 Detailed Solution
\(1 + G\left( s \right)H\left( s \right) = 0\)
\(1 + k\frac{{\left( {{s^2} - 2s + 2} \right)}}{{{s^2} + 2s + 2}} = 0\)
\(k = - \frac{{{s^2} + 2s + 2}}{{{s^2} - 2s + 2}}\)
For break away & break in point differentiating above w. r. t s
\(\frac{{dk}}{{ds}} = - \frac{{\left( {{s^2} - 2s + 2} \right)\left( {2s + 2} \right) - \left( {{s^2} + 2s + 2} \right)\left( {2s - 2} \right)}}{{{{\left( {{s^2} - 2s + 2} \right)}^2}}} = 0\)
\(2{s^3} - 2{s^2} + 4 - \left( {2{s^3} + 2{s^2} - 4} \right) = 0\)
\({s^2} = 2\)
\(s = ± \sqrt 2\)
Angle of departure at pole P, then
\({Q_d} = + 180 + \left( {{\rm{\Sigma }}{\phi _z} - {\rm{\Sigma }}{\phi _p}} \right)\)
\({Q_d} = ± 180 + [(180+135)-90]\)
= ± 45°
Angle of Departure at a Pole Question 8:
A unity feedback system has open loop poles (-2 ± j2) and 0. It has a single zero at (-4 ± j0). The angle of departure of the root locus branch starting from the pole (-2 + j2) is _____ (in degrees)
Answer (Detailed Solution Below) 0
Angle of Departure at a Pole Question 8 Detailed Solution
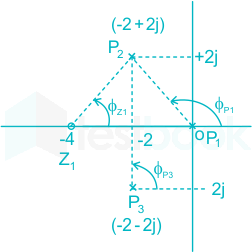
Angle of departure at the pole (-2 + j2)
= 180° - (135°) – 90° + 45°
= 0°
Angle of Departure at a Pole Question 9:
The forward transfer function of a ufb system is \(G\left( s \right) = \frac{{K\left( {s + 2} \right)}}{{\left( {s + 3} \right)\left( {{s^2} + 2s + 2} \right)}}\). The angle of departure from the complex pole is
Answer (Detailed Solution Below)
Angle of Departure at a Pole Question 9 Detailed Solution
Concept:
The angle of departure is tangent to the root locus at the complex poles.
\({\phi _D} = {180^0} + \phi \;;\;\phi = {\phi _z} - {\phi _p}\)
The angle of arrival is tangent to the root locus at the complex zeros.
\({\phi _A} = {180^0} - \phi \;;\;\phi = {\phi _z} - {\phi _p}\)
Where,
ϕZ = Sum of all the angles subtended by the remaining zeros.
ϕP = Sum of all the angles subtended by poles.
Calculation:
poles:-3, -1+j,-1-j
zero = -2
-θ1 - θ2 - θ3 + θ4 = 1800
-θ1 - 900 - tan-1(0.5) + tan-1(1) = 1800
θ1 = -251.60 = 108.40
Angle of Departure at a Pole Question 10:
Angle of departure of the root locus from complex poles of unity feedback control system with open loop transfer function \(G\left( s \right) = \frac{K}{{s\left( {s + 4} \right)\left( {{s^2} + 4s + 5} \right)}}\)
Answer (Detailed Solution Below)
Angle of Departure at a Pole Question 10 Detailed Solution
\(G\left( s \right) = \frac{K}{{s\left( {s + 4} \right)\left[ {s + \left( {2 \pm j} \right)} \right]}}\)
Pole = 0, -4, (-2 ± j)
Angle of departure ϕD = 180 + ϕ
Where, ϕ = [∑∠zero - ∑∠poles]
Sum of angle from poles = [180 – 26.57 + 90 + 26.57]
where 26.57° is the angle made by the pole at -4 with respect to x-axis.
Angle of departure ϕD = 180 – 270 = -90°Angle of Departure at a Pole Question 11:
The open loop Transfer Function of a system is \(\rm {\rm{G}}\left( {\rm{s}} \right){\rm{H}}\left( {\rm{s}} \right) = \frac{K}{{{\rm{s}}\left( {{{\rm{s}}^2} + 2{\rm{s}} + 2} \right)}}\). Then the angle of departure at complex pole \((-1+j)\) is given as
Answer (Detailed Solution Below)
Angle of Departure at a Pole Question 11 Detailed Solution
\(\rm {\rm{G}}\left( {\rm{s}} \right){\rm{H}}\left( {\rm{s}} \right) = \frac{{\rm{K}}}{{{\rm{s}}\left( {{{\rm{s}}^2} + 2{\rm{s}} + 2} \right)}} = \frac{K}{{{\rm{s}}\left( {{\rm{s}} + 1 + {\rm{i}}} \right)\left( {{\rm{s}} + 1 - {\rm{i}}} \right)}}\)
Angle of departure \(= {\left. {180 + \angle {\rm{GH}}} \right|_{{\rm{s}} = - 1 + {\rm{j}}}}\)
\(\angle {\left. {{\rm{GH}}} \right|_{ - 1 + {\rm{j}}}} = \frac{{\rm{K}}}{{\angle \left( { - 1 + {\rm{j}}} \right).\angle 2{\rm{i}}}} = - \left( {\left( {{\rm{\pi }} - \frac{{\rm{\pi }}}{4}} \right) + \frac{{\rm{\pi }}}{2}} \right) = - \frac{{5{\rm{\pi }}}}{4}\)
∴ Angle of departure \(= 180^\circ + \left( { - {{\frac{{5{\rm{\pi }}}}{4}}}} \right)^{\rm{\;c}}\)
\(\rm = 180^\circ - 225^\circ\)
\(\rm = - 45^\circ \)
Angle of Departure at a Pole Question 12:
The angle of departure of complex conjugate poles in the root locus Diagram of a system with open loop transfer function \(\rm {G\left( s \right)H\left( s \right) }= \frac{{K\left( {s + 0.5} \right)}}{{{s^2} + 2s + 2}}\) are
Answer (Detailed Solution Below)
\(206.56°, 153.44°\)
Angle of Departure at a Pole Question 12 Detailed Solution
\(\rm \begin{array}{l} G\left( s \right)H\left( s \right) = \frac{{K\left( {s+ 0.5} \right)}}{{\left( {{s^2} + 2s + 2} \right)}}\\ \rm = \frac{{K\left( {s + 0.5} \right)}}{{\left( {s + 1 + i} \right)\left( {s + 1 - i} \right)}} \end{array}\)
We use the following trigonometric relation to proceed further,
- \(\rm \tan^{-1}(-x)=-tan^{-1}(x)\) and
- \(\rm \tan^{-1}\left(\frac{1}{x}\right)=-\frac{\pi}{2}-\tan^{-1}(x)\)
Thus, \(\rm \tan^{-1}\left(\frac{1}{-x}\right)=-\frac{\pi}{2}-\tan^{-1}(-x)=-\frac{\pi}{2}+\tan^{-1}(x)\)
Proceeding further with this we have,
\(\rm G(s)H(s)\left|_{(s=-1+i)}\right.=\frac{k(i-0.5)}{2i}\)
Thus,
\(\rm ∠G(s) H(s) \ at \ s = -1 + i \ is\)
\(\rm \tan^{-1}\left({\frac{1}{-0.5}}\right)-\tan^{-1}{\left(\frac{2}{0}\right)}= \tan^{-1}\left({\frac{1}{-0.5}}\right)-\frac{\pi}{2}\)
calculating \(\rm \tan^{-1}{\left(\frac{1}{-0.5}\right)}\) separately we have,
\(\rm \tan^{-1}{\frac{1}{-0.5}}=-\frac{\pi}{2}+\tan^{-1}{\frac{1}{2}}=-\frac{\pi}{2}+\left(-\frac{\pi}{2}-\tan^{-1}(2)\right)\)
\(\rm \Rightarrow \tan^{-1}{\left(\frac{1}{-0.5}\right)}=-\pi-\tan^{-1}{2}=2\pi+\left(-\pi-\tan^{-1}{2}\right)\ \ \ \ \left(\because x=2\pi+x\right)\)
\(\rm \Rightarrow \tan^{-1}{\left(\frac{1}{-0.5}\right)}=\pi-\tan^{-1}{2}\)
Thus, \(\rm \tan^{-1}\left({\frac{1}{-0.5}}\right)-\tan^{-1}{\left(\frac{2}{0}\right)}=\pi-\tan^{-1}{2}-\frac{\pi}{2}\)
\(\rm = \pi - {\tan ^{ - 1}}\left( 2 \right) - \frac{\pi }{2} = \frac{\pi }{2} - {\tan ^{ - 1}}\left( 2 \right)\)
Angle of departure at, \(\rm s= -1+i \ is \ 180° + ∠G(s)H(s) \ at \ s = -1 + i\)
i.e \(\rm \phi _d = \left( {180^\circ } \right) + \left( {90 - {{\tan }^{ - 1}}\left( 2 \right)} \right) = 206.56^\circ\)
Similarly Angle of departure at \(\rm s = -1-i\) is
\(\rm \phi _d = \left( {180^\circ } \right) + \left( { - 90 + {{\tan }^{ - 1}}\left( 2 \right)} \right) = 153.44^\circ\)


